SPSS Auswertung - Eine Einführung für Anfänger
- Sebastian Kunzmann

- 11. Aug. 2020
- 8 Min. Lesezeit
Aktualisiert: 10. Apr. 2022
Die Durchführung statistischer Auswertungen in SPSS im Zuge einer empirischen Arbeit (Haus-, Bachelor-, Master- oder Doktorarbeit) bereitet vielen Studenten Probleme. Daher möchten wir Ihnen in diesem Artikel die absoluten Grundlagen der statistischen Datenanalyse mit SPSS vermitteln und eine strukturierte Vorgehensweise aufzeigen.
Sie benötigen Hilfe bei der Datenauswertung in SPSS oder möchten eine SPSS Auswertung (z.B. Fragebogen-Auswertung) bestellen, dann zögern Sie nicht uns zu kontaktieren (Kontaktdaten unten rechts). Unsere Experten helfen Ihnen gerne weiter (kostenloses unverbindliches Erstgespräch)!
1. Vorbereitungen
Bevor wir mit der SPSS Auswertung starten, legen wir zunächst eine Ordnerstruktur für unser Projekt an. Das heißt, dass wir einen Ordner mit einem geeigneten Projektnamen erstellen, welcher die vier Unterordner Daten, Ergebnisse, Code und Sonstiges enthält. Im Ordner Daten speichern wir anschließend unsere Ausgangsdaten und im Ordner Sonstiges beispielsweise die Daten- und Projektbeschreibungen. Der Ordner Code dient dagegen der Speicherung unserer SPSS-Skripte (falls mit Syntaxeditor gearbeitet wird) und der Ordner Ergebnisse ist für den Export der Ergebnisse der SPSS Auswertungen gedacht.
2. Erste Schritte in SPSS
Geschafft! Nun können wir mit der SPSS Auswertung loslegen. Hierzu starten wir SPSS. Grundsätzlich wird in SPSS mit drei Fenstern gearbeitet, nämlich mit Dateneditor, Syntaxeditor und Viewer.
Der Dateneditor erscheint standardmäßig bei Aufruf von SPSS und setzt sich aus der Datenansicht und der Variablenansicht zusammen. Erstere zeigt den Datensatz und Letztere die verschiedenen Variablenattribute. Beim Speichern von SPSS-Datensätzen wird die Dateiendung .sav verwendet. Der Viewer öffnet sich automatisch bei Start einer Analyse und enthält deren Ergebnisse. Viewer-Dateien besitzen die Endung .spv und sollten unbedingt vor Verlassen von SPSS gespeichert werden. Es sei denn, es wird im Syntaxeditor Code geschrieben , so dass sich die SPSS Auswertungen mit nur einem Klick stets wiederholen lassen. Der Syntaxeditor ist in der Regel bei Aufruf von SPSS nicht zu sehen, jedoch kann ein neues Skript via Datei --> Neu --> Syntax geöffnet werden. SPSS-Skripte werden unter der Endung .sps abgespeichert.
SPSS verdankt seine weite Verbreitung in erster Linie seiner grafische Benutzeroberfläche (GUI). Diese ermöglicht Sozial- Wirtschaftswissenschaftlern, Psychologen, und Medizinern die Durchführung von Datenauswertungen in SPSS ohne die Notwendigkeit Programmcode zu schreiben. Konkret, die GUI erleichtert die Bedienung enorm. Dementsprechend nutzt ein Großteil der Anwender den Syntaxeditor in SPSS nicht. Da sich dieser Artikel an SPSS-Anfänger richtet, werden wir im Folgenden hauptsächlich auf die Arbeit mit der GUI und somit die Arbeit im Dateneditor eingehen.
3. Vorstellung des Datensatzes
Da es uns ein großes Anliegen ist, dass der Leser unsere einzelnen Schritte reproduzieren kann, haben wir hier auf dem Import eigener Daten verzichtet. Anstelle dessen verwenden wir den bereits in SPSS enthaltenen Datensatz "marketvalues.sav", welchen Sie im Willkommensfenster unter Stichprobendateien finden. Der Datensatz enthält Informationen zu Hausverkäufen in einem Neubaugebiet in Algonquin, Illinois, in den Jahren 1999–2000.
Ein Klick auf Variablenansicht im Dateneditor liefert das folgende Bild auf Ihrem Bildschirm:

Es ist zu erkennen, dass der Datensatz sieben Variablen enthält. Der Name identifiziert die Variablen eindeutig. Da dieser jedoch lediglich acht Zeichen lang sein darf, findet man eine ausführliche Beschreibung der Variablen in der Regel unter Beschriftung. Die Spalte Typ enthält den Datentyp jeder Variablen und die Spalte Messniveau das Skalenniveau.
In unserem Fall liegen neben dem Kaufpreis (value) die Größe des Objektes (sqft), das Datum des Verkaufes (selldate), die Dauer des Objektes am Markt in Tagen vor dem Verkauf (marktime) sowie die Adressdaten (adress, housenum, street) vor. Ein Blick in den Dateneditor verrät, dass insgesamt 94 Beobachtungen vorliegen. Die folgende Abbildung listet die ersten fünf Beobachtungen im Datensatz auf.

5. Explorative Datenanalyse (EDA)
Nachdem wir uns gerade einen Überblick über die Struktur des Datensatzes verschafft haben, kommen wir nun zur explorativen Datenanalyse. Die explorative Datenanalyse beinhaltet die Berechnung von deskriptiven Statistiken sowie die Erstellung von Grafiken. Da ein zu langer Artikel vermieden werden soll, nehmen wir vereinfachend an, dass unser Datensatz nur den Kaufpreis und die Größe des Objektes beinhaltet. Es soll untersucht werden, ob ein Zusammenhang zwischen dem Kaufpreis eines Hauses und der Größe des Verkaufobjekts besteht.
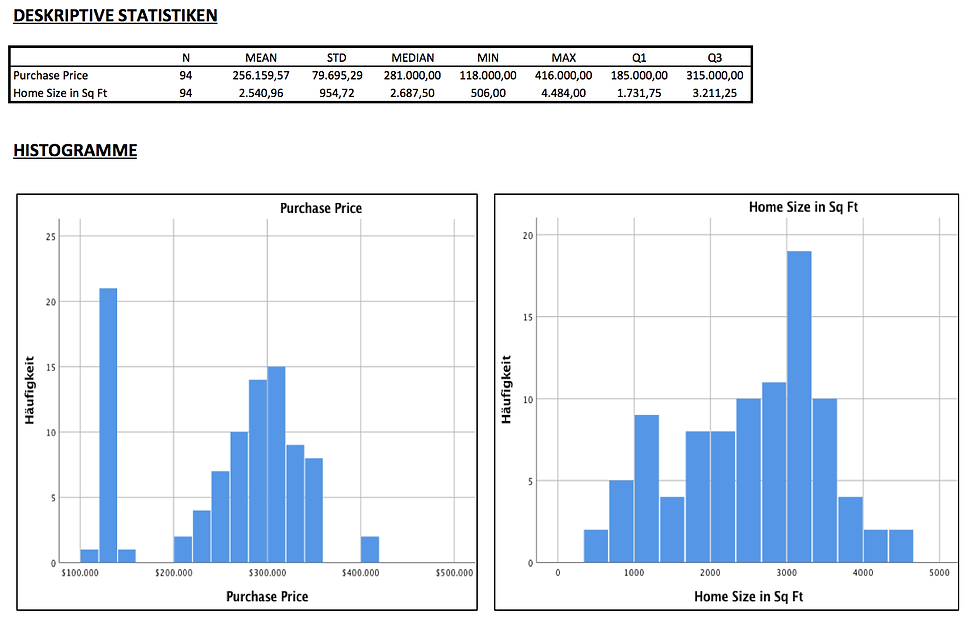
Dementsprechend berechnen wir zunächst die wichtigsten deskriptiven Statistiken der beiden Variablen. Außerdem erstellen wir für beide Variablen Histogramme. Hierzu gehen wir in der Menüleiste auf Analysieren --> Deskriptive Statistiken --> Häufigkeiten. Im sich öffnenden Fenster Häufigkeiten wählen wir die zu analysierenden Variablen aus. Anschließend wählen wir unter Diagramme Histogramm und unter Statistiken die gewünschten Lage- und Streuungsmaße aus.

Schließlich erhalten wir den folgenden Output im SPSS Viewer. Ein Blick auf die deskriptiven Statistiken zeigt, dass der durchschnittliche Kaufpreis eines Hauses im Datensatz 256.159,57 USD beträgt. Der Median liegt mit 281.000 USD leicht über dem Mittelwert. Das günstigste Haus kostete 118.000 USD und das teuerste Objekt 416.000 USD. Darüber hinaus überstieg der Kaufpreis von 25% der Verkaufsobjekte nicht 185.000 USD (Q1). Das obere Quartil (Q3) lag dagegen bei 315.000 USD. Im Histogramm ist außerdem zu erkennen, dass ein relativ großer Anteil der Häuser zwischen 120.000 und 140.000 USD kostete. Durchschnittlich war ein Objekt 2.540,96 sqft groß. Die Streuung (Standardabweichung) der Hausgröße betrug 954,72 sqft. Das kleinste Verkaufsobjekt wies 506 sqft und das größte Objekt 4.484 sqft auf.
Nachdem wir die beiden Variablen detailliert für sich analysiert haben, widmen wir uns nun der Analyse des Zusammenhanges zwischen den beiden Variablen. Hierzu erstellen wir zunächst ein Streudiagramm (Scatterplot), indem wir über Grafik --> Diagrammerstellung das folgende Fenster öffnen.
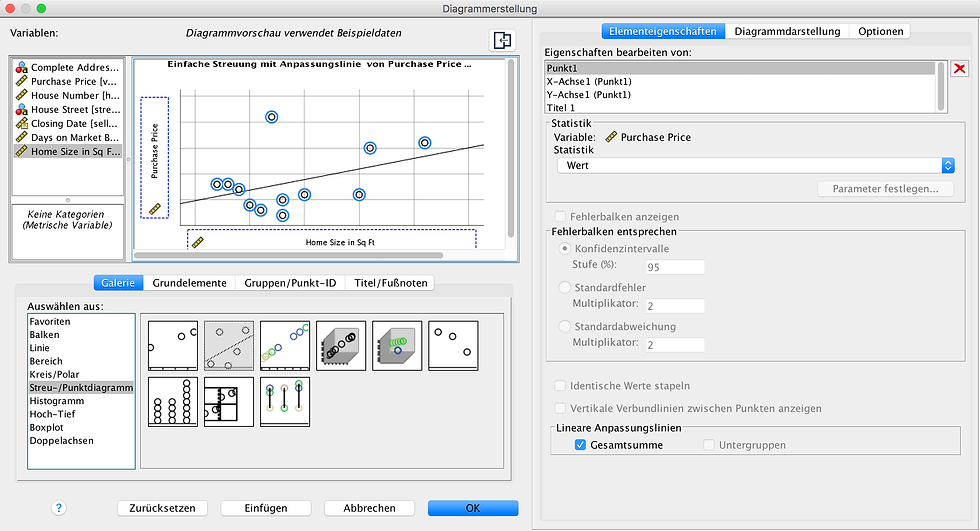
Nachdem der gewünschte Plot (hier: Streudiagramm mit linearer Regressionslinie) unten links ausgewählt und die Hausgröße auf die x- Achse sowie der Kaufpreis auf die y-Achse gezogen wurden, wird das folgende Streudiagramm erstellt.

Es zeigt sich, dass ein höhere Anzahl an sqft mit einem größerem Verkaufspreis einhergeht. Außerdem ist zu erkennen, dass die lineare Regressionsgerade eine sehr gute Anpassungsgüte aufweist. Lediglich die Verkaufspreise von kleineren Objekte werden im Durchschnitt leicht überschätzt. Das Bestimmtheitsmaß dieser einfachen linearen Regression beträgt 0,8. Folglich werden 80% der Streuung der Kaufpreise durch die Größe des Objektes erklärt.
5. Regressionsanalyse
Wie wir gerade festgestellt haben, steigt der Kaufpreis mit der Größe eines Objektes an. Um den Einfluss der Größe eines Objektes auf den Kaufpreis zu quantifizieren, kann eine Regression durchgeführt werden. Im Zuge der Regressionsanalyse wird die obige lineare Regressionslinie bestimmt. Konkret wird der Achsenabschnitt und die Steigung der Gerade ermittelt. Dabei gilt es zu beachten, dass wir damit implizit annehmen, dass die Größe kausal für den Preis ist und nicht ein umgekehrter Zusammenhang vorliegt. Diese Annahme ist für unser Beispiel allerdings durchaus realistisch und stellt somit kein Problem dar.
Aufgrund der beobachteten leichten durchschnittlichen Überschätzung der Verkaufspreise von kleineren Objekten, nehmen wir in unsere Regressionsgleichung zusätzlich die quadrierte Hausgröße auf. Damit kann der Tatsache Rechnung getragen werden, dass der Preis pro sqft in der Regel mit zunehmender Größe abnimmt. Folglich unterstellen wir für die Kaufpreise folgenden datengenerierenden Prozess (DGP):

Wir nehmen also an, dass sich der Kaufpreis von Haus i gemäß obiger Gleichung ergibt. Der letzte Term wird als Fehlerterm (Störgröße) bezeichnet und es wird angenommen, dass dessen Erwartungswert Null ist. Im Zuge einer Regression werden die drei Beta-Parameter geschätzt. Zur Durchführung dieser multiplen linearen Regression berechnen wir zunächst das Quadrat der Hausgröße, welches den Variablennamen sqft2 erhält. Dazu gehen wir zu Transformieren --> Variable berechnen.

Um nun die Regressionsanalyse durchzuführen, gehen wir auf Analysieren --> Regression --> Linear. Anschließend wählen wir den Kaufpreis (value) als abhängige Variable und die Größe (sqft) sowie dessen quadrierte Ausprägung (sqft2) als unabhängige Variablen. Für die spätere Modellvalidierung empfiehlt es sich den "Standardized Residuals vs. Standardized Fitted" Plot zu erstellen, indem ZPred im Fenster Diagramme auf die x-Achse und ZRESID auf die y-Achse gezogen werden. Außerdem setzen wir zur Erstellung eines P-P-Plots einen Haken bei "Normalverteilungsdiagramm".

Die folgende Abbildung zeigt den Teil des Resgressionsoutputs mit den Parameterschätzungen. Der Schätzwerte der Parameter sind in der zweiten Spalten zu finden. Die zugehörigen geschätzten Standardfehler der Koeffizienten finden Sie dagegen in Spalte 3. Der Standardfehler ist ein Maß für die Präzision der Schätzung eines Koeffizienten. Je höher der Standardfehler, desto höher ist die Schätzunsicherheit.

Um zu ermitteln, ob ein Regressor einen statistisch signifikanten Einfluss auf die Zielgröße hat, wird ein t-Test durchgeführt. Dieser testet, ob der Regressionskoeffizient der entsprechenden erklärenden Variable statistisch signifikant von Null verschieden ist. Die Teststatistik dieses parametrischen Tests ergibt aus der Division der Schätzwerte für den Koeffizienten und den zugehörigen Standardfehler. Mit Hilfe der Teststatistik kann anschließend der P-Value aus der t-Verteilung mit (n-k) Freiheitsgraden ermittelt werden, wobei n die Anzahl der Beobachtungen im Datensatz und k die Anzahl der zu schätzenden Regressionskoeffizienten ist. Der P-Value stellt das größtmögliche Signifikanzniveau (Irrtumswahrscheinlichkeit) dar, bei dem die berechnete Teststatistik gerade noch nicht zu einer Ablehnung der Nullhypothese geführt hätte. Ist der P-Value kleiner als das vor dem Test festgelegte Signigikanzniveau (idR: 5%), dann wird die Nullhypothese, dass die entsprechende erklärende Variable keinen Einfluss hat, verworfen. Die Teststatistiken und P-Werte sind in den letzten beiden Spalten der Tabelle zu finden.
In unserem Beispiel ist zu erkennen, dass sich der Achsenabschnitt nicht statistisch signifikant von 0 unterscheidet. Die P-Values der Größe und dessen quadrierter Version sind dagegen kleiner als 5% und somit haben die beiden Features einen statistisch signifikanten Einfluss auf die Kaufpreise. Da die Variable Größe auch quadratisch in das Modell eingeht, hängt der partielle Effekt der Größe auf den Kaufpreis vom Niveau der Größe ab. Eine ein sqft größere Wohnung kostet durchschnittlich (113,507 + 2 x (-0,008) x sqft) USD mehr. Folglich nimmt der Kaufpreis pro sqft mit zunehmender Objektgröße ab.
Das Bestimmtheitsmaß unseres Regressionsmodelles liegt bei 81%. Allerdings haben wir bei unserer bisherigen Analyse einen wichtigen Schritt vergessen. Es wurde nicht überprüft, ob die Annahmen des linearen Regressionsmodells und die des t-Tests erfüllt sind. Dementsprechend holen wir das nun nach.
Zunächst wird die Annahme der korrekten Spezifikation überprüft. Diese besagt, dass der DGP (datengenerierende Prozess) im Modell enthalten sein muss, wenn die geschätzen Parameter den wahren Parameter entsprechen würden. Das bedeutet konkret, dass in im Modell keine Einflussfaktoren fehlen dürfen und das die unterstellte lineare Form der des DGP entsprechen muss. Da der DGP allerdings unbekannt ist, ist diese Annahme schwierig zu überprüfen. Eine Möglichkeit zur Prüfung der Annahme ist die Betrachtung des "Standardized Residuals vs. Standardized Fitted" Scatterplot, in dem die standardisierten Residuen auf die standardisierten geschätzten Werte der Zielgröße abgetragen werden. Die Residuen sind die beobachteten Fehler, d.h. die Differenz aus den Beobachtungen und den jeweiligen Schätzungen der Zielgröße. Unter Standardisierung versteht man dagegen die Transformation einer Zufallsvariable, so dass die resultierende Zufallsvariable einen Erwartungswert von null und eine Varianz von eins besitzt.

Im "Standardized Residuals vs. Standardized Fitted" Scatterplot ist zu erkennen, dass die Punkte relativ unsystematisch um die horizontale Nulllinie streuen. Dementsprechend wird die abhängige Variable von unserem Modell nicht systematisch unter- bzw. überschätzt und somit kann anhand der Daten nicht die korrekte Spezifikation des Modells widerlegt werden.
Anhand dieses Scatterplot kann auch die Annahme homoskedastischer Fehler überprüft werden. Die Fehler werden als homoskedastisch bezeichnet, wenn deren Varianz für alle Stichprobenbeobachtungen unabhängig von der Hausgröße konstant ist. Ist das nicht der Fall, dann spricht man von Heteroskedastie. In unserem Beispiel ist die Streuung der Punkte um die horizontale Nullinie relativ konstant und somit kann die Annahme homoskedastischer Fehler anhand der Daten nicht widerlegt werden.
Abschließend ist noch die Annahme bedingt normalverteilter Fehler zu überprüfen. Dabei handelt es sich um eine Annahme des t-Tests und nicht um eine des Regressionsmodells. Zur Prüfung dieser Voraussetzung wird der P-P-Plot betrachtet, welcher die beobachteten kumulierten Wahrscheinlichkeiten der standardisierten Residuen mit denen der Standardnormalverteilung vergleicht. Alternativ hätte auch der in der Praxis häufiger verwendete Q-Q-Plot der standardisierten Residuen zur Überprüfung der Annahme verwendet werden können.

Im P-P-Plot ist zu erkennen, dass die beobachteten kumulierten Wahrscheinlichkeiten der standardisierten Residuen relativ gut mit denen der Standardnormalverteilung übereinstimmen. Folglich kann anhand des Diagramms die Annahme bedingt normalverteilter Fehler nicht widerlegt werden.
Aufgrund der erfolgreichen Prüfung der Annahmen kann also festgehalten werden, dass das in diesem Artikel spezifizierte lineare Regressionsmodell valide ist und das die berechneten p-Values der t-Tests korrekt sind.
Zusammenfassung -Key Facts
In diesem Artikel haben wir Studenten eine strukturierte Vorgehensweise für die Datenanalyse aufgezeigt, welche sie in einer empirischen Haus-, Bachelor- oder Masterarbeit anwenden können. Darüber hinaus wurden Ihnen die Grundlagen der Datenauswertung mit SPSS vermittelt. Leser dieses Artikels sollten nun selbstständig einfache SPSS Auswertungen durchführen können.
Der Abschnitt Regressionsanalyse ist für Anfänger sicherlich keine leichte Kost, zeigt aber aus unserer Sicht wichtige Aspekte einer statistische Auswertung auf. Es war uns wichtig zu zeigen, dass zur Anwendung populärer statistischer Methoden (z.B. Regression) auch die Überprüfung von Annahmen gehört. Ansonsten können schnell falsche Schlussfolgerungen gezogen werden.
Wir hoffen, dass Ihnen dieser Artikel bei Ihren ersten SPSS Auswertungen weiterhilft. Falls Sie Probleme mit einer statistischen Auswertung in Ihrer Arbeit haben, zögern Sie nicht uns zu kontaktieren. Unser Team an Freelancern verfügt über langjährige Erfahrung auf dem Gebiet der Datenanalyse in SPSS. Wir beraten Sie gerne bei Ihrem statistischen Problem. Darüber hinaus können Sie bei uns auch SPSS Auswertungen inkl. verständlicher Interpretationen bestellen (z.B. Fragebogen-Auswertungen). Gerne bieten wir Ihnen hierfür ein kostenloses und unverbindliches Erstgespräch mit einem unserer Experten an. Sie können uns jederzeit per E-Mail oder Telefon (siehe unten rechts) erreichen.
Kommentare